เมื่อเราสร้างชุด Seed ด้วยตนเองได้แล้ว หรืออาจจะได้มาจากการสุ่มของ Hardware Wallet ใด ๆ ก็ตาม ต่อไปจะเป็นการนำ Seed ผ่านกระบวนการทางคณิตศาสตร์มากมาย เพื่อไปสู่ Public Key
ในที่นี้ขอให้คิดว่า Seed เป็นตัวเลขที่ได้จากการสุ่ม ซึ่งมันก็สุ่มมาจริง ๆ (จะบอกอีกรอบทำไม)
อย่างที่เรารู้จักกันดี Bitcoin Wallet จะสร้าง Public Key และ Private Key ขึ้นมาคู่กัน ซึ่งการได้มาของกุญแจทั้งสองดอกนี้มีวิธีการทางคณิตศาสตร์อยู่เบื้องหลัง (กำลังจะเริ่มแล้ว ทำใจนิดนึง) เราต้องรู้จักกับคณิตศาสตร์ที่ใช้ในระบบ Bitcoin ก่อน มาทำความรู้จักทีละอย่างไปพร้อม ๆ กันนะครับ (ขอให้ทุกคนเปิดใจกับคณิตศาสตร์มันไม่ยากขนาดที่คุณคิด ใครที่อ่านแล้วยังไม่เข้าใจมากแนะนำให้อ่าน 2 – 3 รอบแล้วคุณจะตะโกนออกมาว่า “อ๋อ แบบนี้นี่เอง” //เจ้าของบทความกำลังภาวนา)
โดยระบบเบื้องหลังนี้เรียกว่า ECDSA ย่อมาจาก Elliptic Curve Digital Signature Algorithm ซึ่งในบทความนี้ เราจะกล่าวถึง Elliptic Curve ก่อน Digital Signature จะตามมาในภายหลังครับ
Elliptic Curves
โค้งรูปไข่ (Elliptic Curves) เป็นความสัมพันธ์อย่างหนึ่ง ซึ่งกำหนดให้ y^2 = x^3+ax+b โดยที่ a, b เป็นสมาชิกของจำนวนจริงใด ๆ
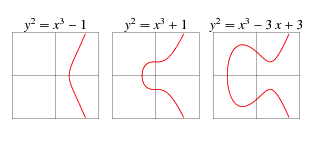
รูปตัวอย่างของ Elliptic Curves
จากการสังเกตจะเห็นว่าทุก Elliptic Curves จะสมมาตรในแนวแกน X
นิยามการบวกของจุด
สมมติจุด P และจุด Q เป็นจุดใด ๆ บนเส้นโค้ง
จุด P+Q สามารถหาได้จากการลากเส้นตรงตัดผ่านจุด P และจุด Q (มีเพียงเส้นเดียวเท่านั้น) จะตัดเส้นโค้งที่จุด -(P+Q) จากนั้นสะท้อนจุดดังกล่าวกับแกน X จะได้จุด P+Q
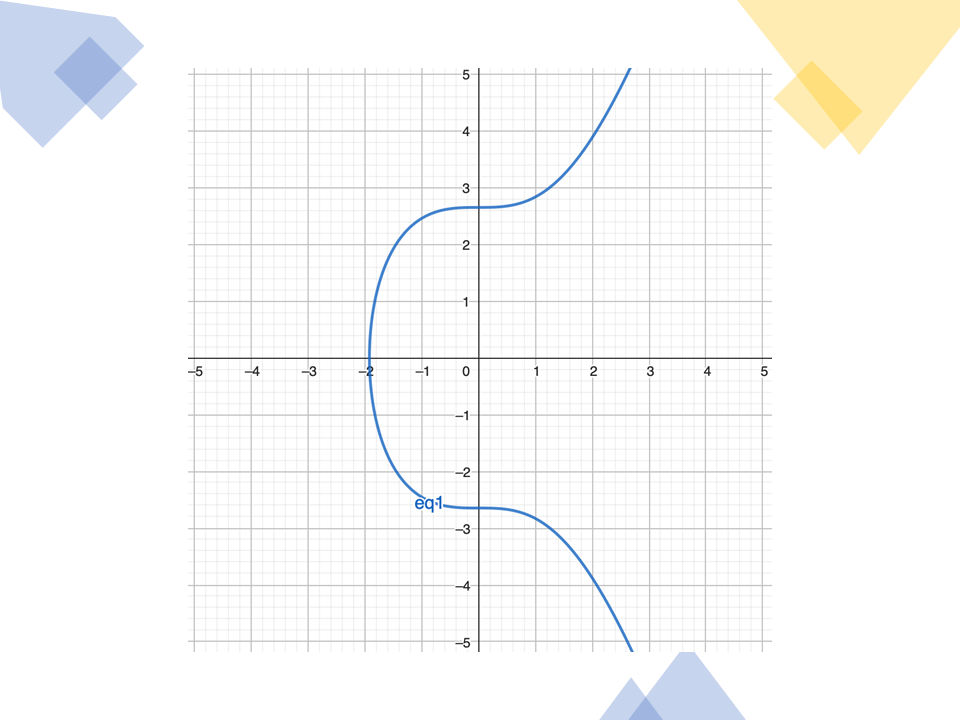
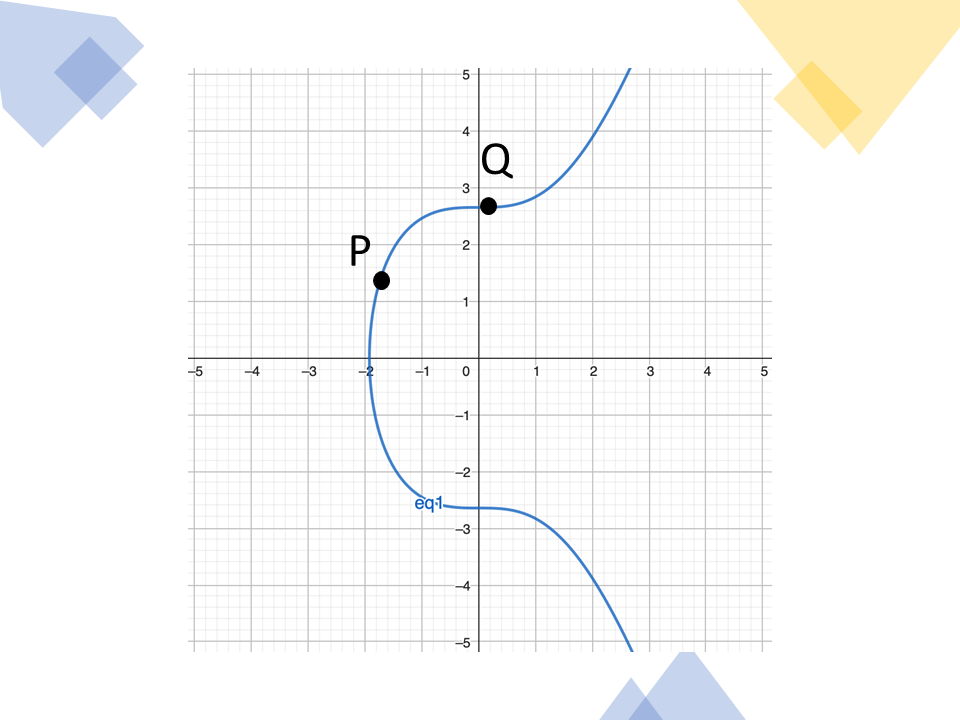
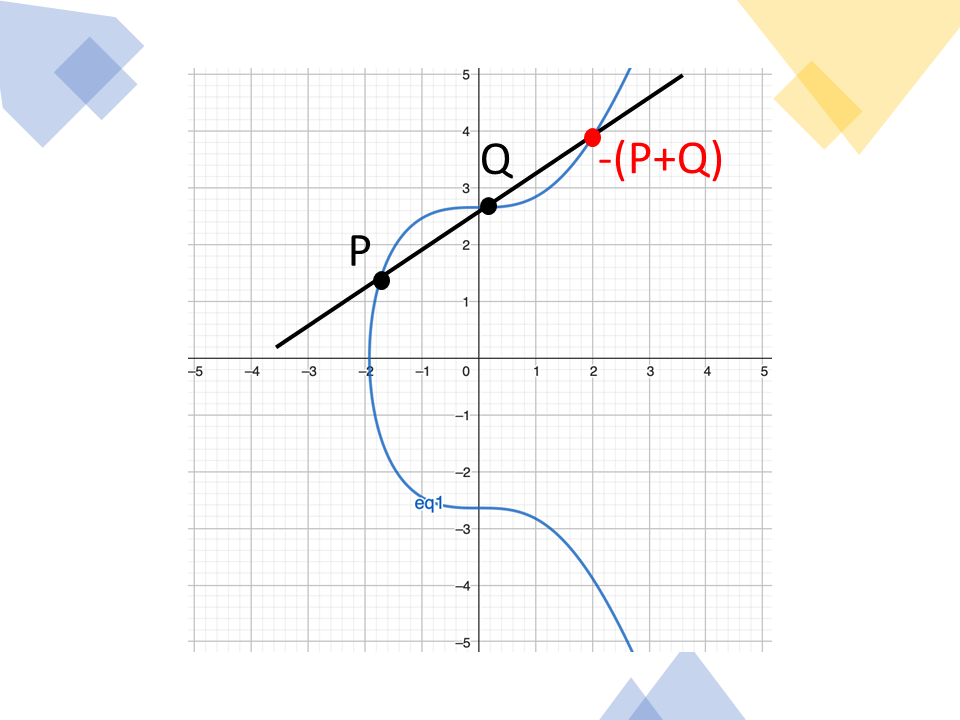
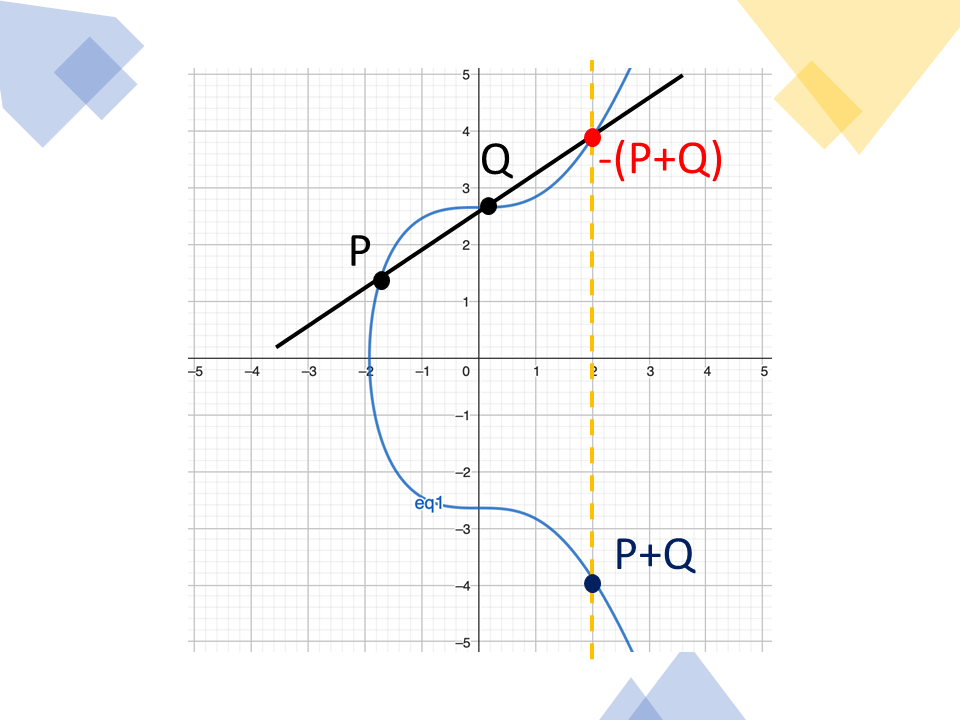
ภาพอธิบายการบวกของจุด
นิยามการคูณของจำนวนกับจุด
ทบทวนการคูณพิจารณา 2 x 3 = 6 ซึ่งตามนิยามการคูณแล้ว 2 x 3 = 3 + 3
เมื่อเราพิจารณาการคูณใน Elliptic Curves สมมติจุด G เป็นจุดใด ๆ บนเส้นโค้ง
จุด 2G สามารถหาได้จากการพิจารณา 2*G = G + G นั่นคือการลากเส้นตรงซึ่งสัมผัสกับจุด G (มีเพียงเส้นเดียวเท่านั้น) จะตัดเส้นโค้งที่จุด -2*G จากนั้นสะท้อนจุดดังกล่าวกับแกน X จะได้จุด 2*G
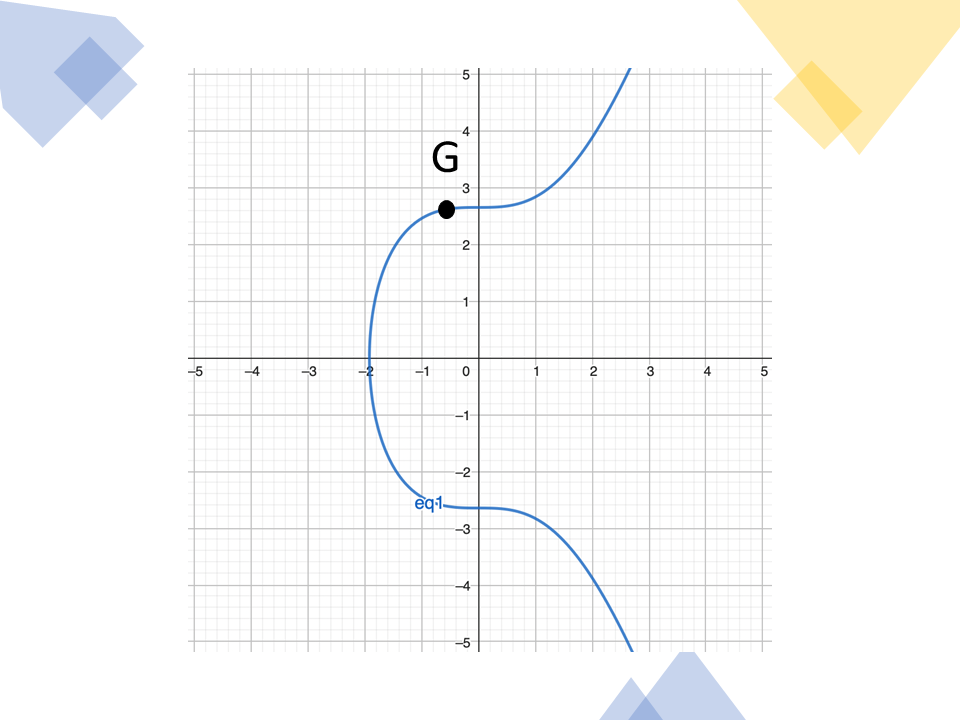
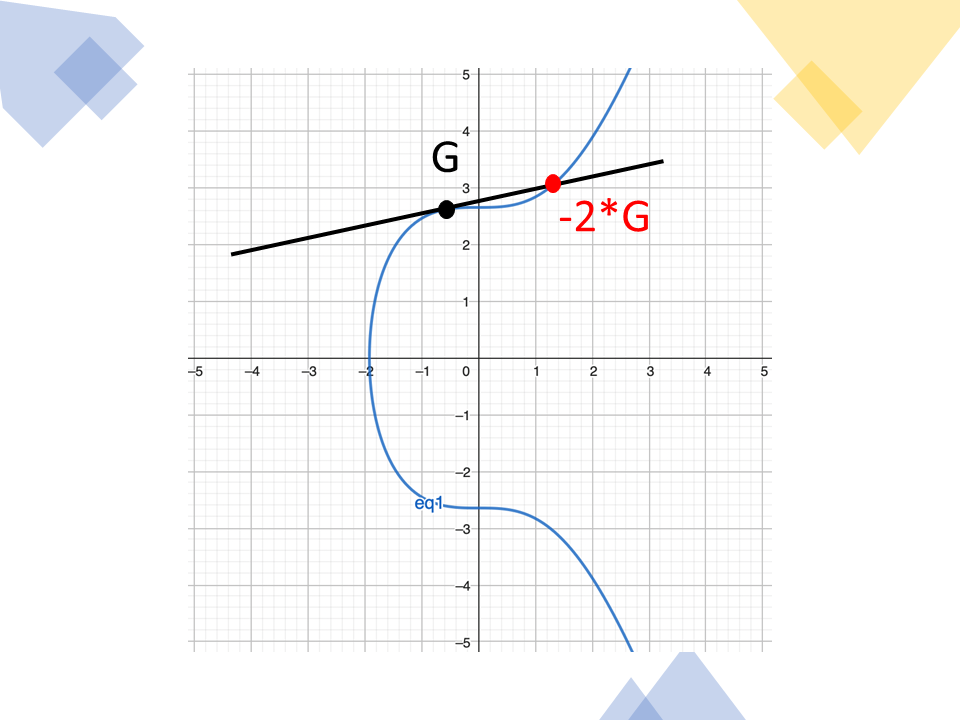
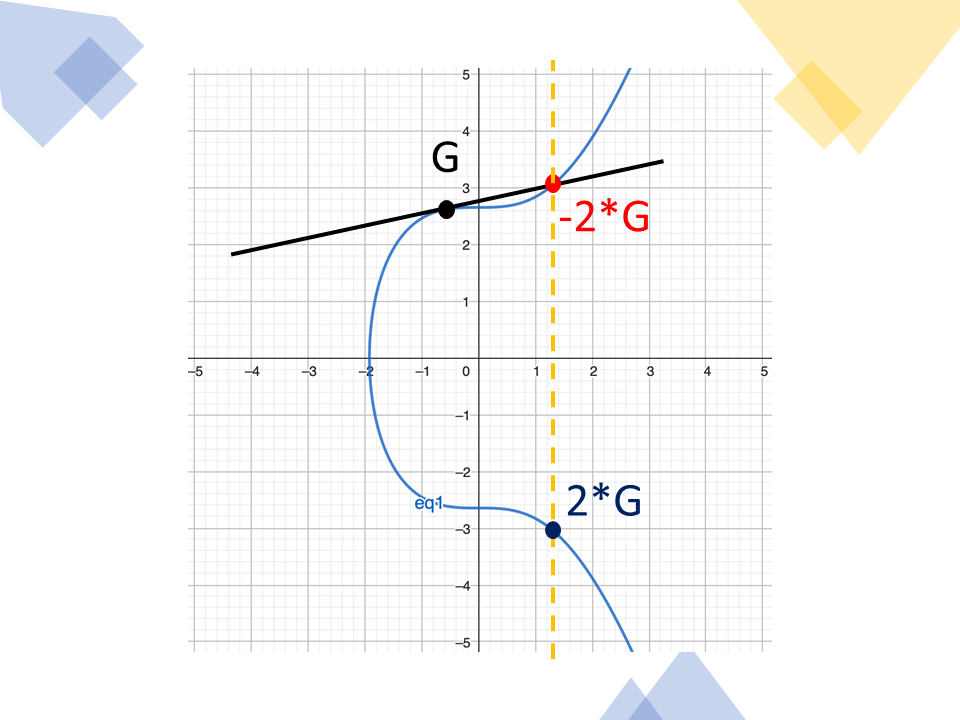
ภาพอธิบายการคูณของจำนวนกับจุด
เขียนจำนวนที่ต้องการให้อยู่ในรูปของการบวกและการคูณ
เพื่อให้ง่ายต่อการคำนวณในระบบ ถ้าผมต้องการหาจุด 11G ผมสามารถหาได้จากการพิจารณา 11*G = 2*(2*(2*G)+G)+G นั่นคือ ทุกคนสามารถหาจุด 14*G 169*G หรือแม้กระทั้ง 23589*G ได้แล้วใช่ไหมครับ เพราะมันคือการหาจากการเขียนจำนวนนั้นให้อยู่ในรูปการบวกและการคูณ และทำตามกระบวนการที่ได้กล่าวไปข้างต้น
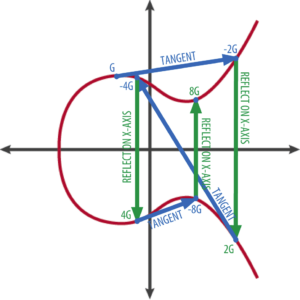
ภาพอธิบายการหา n*G ในที่นี้ยกตัวอย่าง 8*G
แบ่งกลุ่มของจำนวนโดยใช้การหารเอาเศษ
ต่อไปเราจะกล่าวถึงเซต (กลุ่มของสิ่งของต่าง ๆ ในที่นี้จะหมายถึง กลุ่มของจำนวนต่าง ๆ) และจำนวนนับ (1, 2, 3, … ) เราจะนำเซตมาแบ่งส่วนภายในเป็น n ส่วน แล้วจะบอกว่ามีจำนวนไหนอยู่ส่วนใดได้บ้าง โดยที่วิธีการหารเอาเศษ (MOD) ยกตัวอย่างเช่น ในกรณีที่ต้องการแบ่งเซตออกเป็น 4 ส่วน
- ส่วนที่ 1 ตั้งชื่อว่า (เหลือเศษเป็น 1)
- ส่วนที่ 2 ตั้งชื่อว่า (เหลือเศษเป็น 2)
- ส่วนที่ 3 ตั้งชื่อว่า (เหลือเศษเป็น 3)
- ส่วนที่ 4 ตั้งชื่อว่า (หารด้วย 4 ลงตัว)
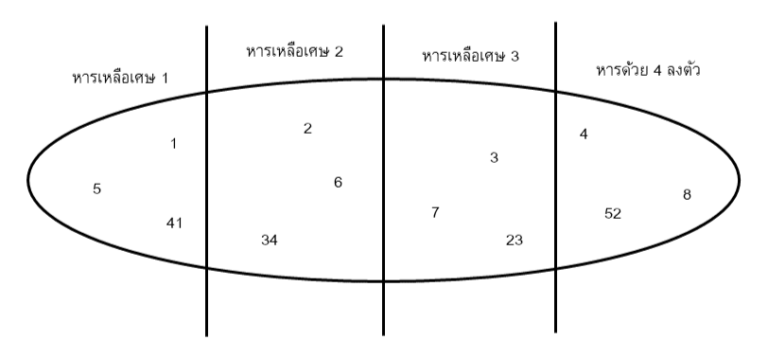
เซตของจำนวนนับซึ่งถูกแบ่งเป็น 4 ส่วน
ถ้าต้องการทราบว่า 23 อยู่ส่วนใด ให้นำ 23 หารด้วย 4 จะได้ผลลัพธ์คือ 5 เศษ 3 นั่นคือ 23 อยู่ส่วนที่ 3 วิธีการนี้สามารถบอกได้ว่าจำนวนที่เราสนใจอยู่ส่วนไหน
ถ้ายังนึกภาพไม่ออกให้คิดว่าไปค่ายลูกเสือและให้แบ่งกลุ่มโดยต้องการ 4 กลุ่ม ให้นับ 1 – 4 วนไปเรื่อย ๆ พอนับถึง 4 ให้คนต่อไปกลับมานับ 1 และนับต่อไปเรื่อย ๆ จนครบจำนวนคน
เนื่องจากเราสามารถหาค่าจุด i*G โดยที่ i เป็นจำนวนนับได้แล้ว จากการเริ่มพิจารณาแค่จุดแรกจุดเดียว (จุด G) ทำให้ได้ผลลัพธ์หลายแบบแต่ผลลัพธ์ที่ได้นั้นยังซ้ำกับผลลัพธ์ที่เคยหามาก่อนหน้านี้แล้วทำไปซ้ำ ๆ ก็ยังวนลงแบบนี้เป็นกลุ่ม ๆ ดังตัวอย่าง
ถ้าเราพิจารณา y^2 = x^3+7 (mod 17) [p = 17] จะได้กราฟดังรูป ซึ่งได้กำหนดจุด G เป็นจุดเริ่มต้นแล้ว จะได้จุด 2*G จุด 3*G จุด 4*G ไปเรื่อย ๆ จนถึง 17*G (ใช้กระบวนการเดิม) แล้ววนกลับมาที่จุด G ทำเช่นนี้ไปเรื่อย ๆ จะเกิดจุดผลลัพธ์ที่ซ้ำกัน
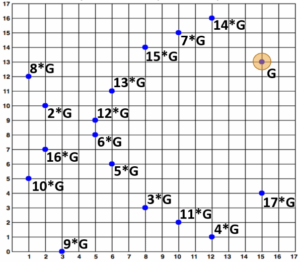
จุดต่าง ๆ ของ y^2=x^3+7 บน F17
จะเห็นได้ว่ามีจุดผลลัพธ์ทั้งหมด 17 จุด บนแกน X ยกเว้น x = 0, 4, 7, 9, 11,13, 14 และ 16 แต่จะไม่นับ 17 เพราะ 0 และ 17 หารด้วย 17 ลงตัวทั้งสองจำนวน จากที่เราแบ่ง 17 กลุ่มได้ใช้งานเพียง 9 กลุ่มเท่านั้น [n = 9] อีก 8 กลุ่มไม่มีสมาชิกอยู่เลย ซึ่งแต่ละกลุ่มประกอบไปด้วยสมาชิก 1 – 2 จุด
จุดแต่ละจุดมีความน่าจะเป็นที่เราจะสุ่มได้จุดนั้น เท่ากับ (1/17 มีค่าประมาณ 5.88%) ถึงแม้ว่าเราจะรู้ว่าจุดนั้นอยู่ตำแหน่งใดแต่ก็ยังไม่สามารถทราบได้อยู่ดีว่ามันคือ i*G ที่มีค่า i เท่ากับเท่าใด
นี่คือกระบวนการที่มีแบบแผนชัดเจนทำจากหน้าไปหลังได้สบาย ๆ แต่ไม่สามารถย้อนกลับกระบวนการนี้ได้ ไม่ว่าจะในเชิงพีชคณิตหรือเรขาคณิต (ไว้อธิบายเพิ่มเติมในบทความแบบไม่ง่าย ฝากติดตามด้วยนะครับ ในบทความนี้จะอธิบายในบางส่วน) เช่น เมื่อเราจะย้อนกลับกระบวนการ สุ่มจุดมา 1 จุด (ที่เราเห็นว่ามีจริง) บนกราฟ การสะท้อนจุดนั้นข้ามแกน X นั่นสามารถทำได้ แต่การหาเส้นตรงที่ลากผ่านจุดนั้น แล้วตัดหรือสัมผัสกราฟ ไม่สามารถทำได้ เนื่องจากมีเส้นตรงที่ตัดหรือสัมผัสกราฟมากมายหลายเส้น ต้องรู้ก่อนว่าต้องตัดหรือสัมผัสกราฟที่จุดใดบ้าง ถึงจะหาเส้นตรงเส้นนั้นได้ แต่เราไม่อาจทราบได้ว่าต้องตัดหรือสัมผัสกราฟที่จุดใดจริง ๆ
Elliptic Curves on Finite Field (Fp)
ในการคำนวณของจำนวนต่อไปนี้ เราจะไม่พิจารณาเป็นจำนวนจริงอีกต่อไป เนื่องจากจำนวนจริง ซึ่งประกอบด้วยจำนวนตรรกยะ (เขียนให้อยู่ในรูปเศษส่วนได้) และจำนวนอตรรกยะ (เขียนให้อยู่ในรูปเศษส่วนไม่ได้หรือทศนิยมไม่ซ้ำ) ล้วนทำให้คอมพิวเตอร์คำนวณได้ช้า เพราะ แท้จริงแล้วคอมพิวเตอร์ทำงานบนเลขฐานสอง (0 และ 1) ซึ่งแปลงให้เป็นจำนวนเต็ม (เลขฐานสิบ) แล้วสามารถคำนวณได้เร็วกว่า ดังนั้น เราจะพิจารณาเป็นจำนวนเต็ม (เลขฐานสิบ) เพื่อความสะดวกต่อความเข้าใจ
Bitcoin ใช้ Elliptic Curves ที่เฉพาะเจาะจงและทุกคนสามารถตรวจสอบได้ นั่นคือ secp256k1 ซึ่งนิยามโดย y^2 = x^3+7 บน Fp หรือ y^2 (mod p) = x^3+7 (mod p)
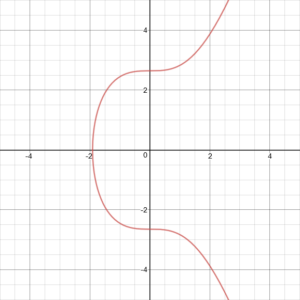
Elliptic Curves : y^2 = x^3+7
ซึ่ง p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663 (จำนวนเฉพาะที่ใหญ่มาก ใหญ่ขนาดไหน ลองจินตนาการดูว่าจำนวนเม็ดทรายทั้งโลกยังไม่มากเท่าจำนวนนี้)
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337 (prime number)
และกำหนดจุด G คือจุด (x = 55066263022277343669578718895168534326250603453777594175500187360389116729240, y = 32670510020758816978083085130507043184471273380659243275938904335757337482424)
การสร้าง Public Key
เราสามารถสร้าง Public Key ได้จากกระบวนการที่ได้กล่าวมาข้างต้น โดยอิงจากสมการ
- Private Key (เลขฐานสิบ) : privKey คือ รูปแบบหนึ่งของ Seed (ย้อนกลับไปอ่านบทความของคุณ Gracialo679) ที่อยู่ในรูปเลขฐานสิบ
- Public Key (Elliptic Curves Point): pubKey = privKey * G
เมื่อเราได้ PrivKey มาแล้วจากการสุ่ม นำจำนวนเต็มดังกล่าวมาคูณกับจุด G ซึ่งนิยามบน Elliptic Curves y^2 = x^3+7 บน Fp โดยเขียนจำนวนเต็มดังกล่าวให้อยู่ในรูปของการบวกและการคูณ จากนั้นใช้นิยามการบวกและการคูณของจำนวนกับจุด ในการหาจุด privKey * G นั่นคือ เราจะได้ pubKey หรือ Public Key แล้ว ยินดีด้วยครับ
ยกตัวอย่างเช่น นาย A มี Seed (24 คำ) ดังนี้
“original destroy course whale term stuff
place cloth indoor sketch reunion penalty
lock cube depth alcohol just novel
boat column bridge tray gadget forum”
นำ Seed มาเขียนให้อยู่ในรูปเลขฐานสอง จะได้
“10011100101 00111100001 00110001010 11111001101 11011111011 11010111100
10100101110 00101011110 01110011000 11001010001 10111000010 10100010100
10000011011 00110101011 00111011001 00000110000 01111001011 10010111000
00011000110 00101101110 00011011110 11100111101 01011110101 010”
จากนั้น เขียนให้อยู่ในรูปเลขฐานสิบ (จำนนวนเต็ม)
“70856784193584852859273959719464926870872514707760377748055530373471294937002” ซึ่งแทนด้วยตัวแปร privKey
นำ privKey * G ได้ผลลัพธ์เป็นจุดซึ่งมีพิกัด ดังนี้
(x = 24285508465354050419380327278877037448923482296870948776717927292815782831762, y = 108442291426069491982935495926891709530887506734116223489130300136669401900375) ซึ่งเป็น pubKey ของนาย A นั่นเอง
**หมายเหตุ ECDSA ฉบับเต็ม secg.org (Bitcoin ใช้เพียง 2.4.1 Recommended Parameters secp256k1 อย่างเดียว) **
ไม่ยากเกินกว่าจะเข้าใจใช่ไหมครับ ตอนแรกอาจจะงงว่ารู้ไปทำไม พออ่านจบจะขมวดความรู้ทั้งบทความได้โดยใช้สมการเพียงสมการเดียว ในที่นี้เราได้ Public Key แล้วเรียบร้อย หนทางต่อไปคือต้องหา Address ที่ไว้ใช้รับ – ส่งเงินของเรา ซึ่งจะต้องอธิบายต่อใน ทำความเข้าใจหลักการทำงานเบื้องหลัง (ของเบื้องหลัง) ของ Bitcoin Part 2 ทำความรู้จักไปทีละขั้นตอนครับ และจะนำไปสู่การอธิบาย Digital Signature กับคำที่ Bitcoiner มักพูดอยู่บ่อย ๆ คือ “Don’t Trust, Verify” ใน Part 3